RSA

文章发布时间:

最后更新时间:

文章总字数:
449

预计阅读时间:
1 分钟

RSA基本原理

接触了半年ctf 现在才开始学rsa 233 倒也不为晚 刚好重新学逆向的时候遇到了rsa的题目 那就顺便来学习一下

rsa的加密实际上就是由明文进行E次方后和N进行取模运算

1
密文＝(明文^E)modN

其中E和N被合称为公钥 记作 (E,N)

而解密也可以看作和加密一样 由密文进行D次方后和N进行取模运算得到

1
明文＝密文^DmodN

相应的 D和N合称为私钥 记作 (D,N)

密钥对则是公钥和私钥的合并 记作（E，D，N）

密钥对的生成一共要经过四个步骤 其中还需要一个中间数 这里记作L

依次是 求N 求L 求E 求D

求N N实际上是由两个质数相乘得到 可以记作 N = P*Q

求L L是q-1和p-1的最小公倍数 L=lcm（p－1，q－1）

求E E比1大比L小 E和L的最大公约数为1 gcd（E，L）=1

求D D要根据E来计算出来 E＊D mod L ＝ 1

例题

比如buu上的一题RSA 给了两个附件 一个存放密文 一个存放公钥

去这个网站把公钥分解一下

RSA公私钥分解 Exponent、Modulus，Rsa公私钥指数、系数(模数)分解–查错网 (chacuo.net)

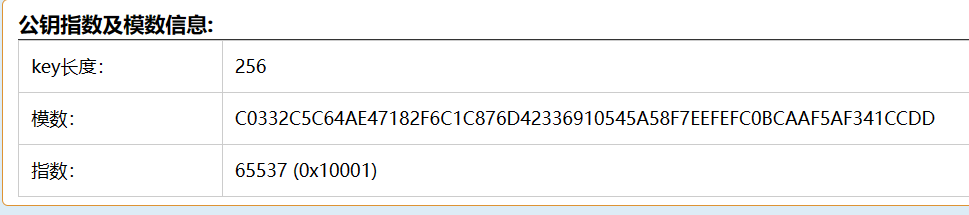
image-20230327155727128

将模数转化为十进制后 就是N 指数则为E

factordb.com这个网站可以拆解N 得到pq

1
2
p= 285960468890451637935629440372639283459
q= 304008741604601924494328155975272418463

接着进行简单的脚本运算就可以得到明文

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import gmpy2
import rsa

e = 65537
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463

phin = (q-1)*(p-1)
d = gmpy2.invert(e, phin)

key = rsa.PrivateKey(n, e, int(d), p, q)

with open("C:\\Users\\22346\\Desktop\\flag.enc", "rb+") as f:
    f = f.read()
    print(rsa.decrypt(f, key))
≡